This report is automatically generated with the R package knitr (version 1.28) .

###########################################################
###########################################################
############ NAME GENDERING EXPERIMENT RESULTS ############
###########################################################
###################### LISA SULLIVAN ######################
###################### July 13, 2020 ######################
###########################################################
###########################################################

#########################################################
######### READ IN LANGUAGE SPECIFIC DATA FILES ##########
#########################################################
setwd("~/Documents/GP2/expt")
read.delim("english_data_all.txt",header=T,as.is = T, comment.char = "#" )->dat_en
read.delim("korean_data_all.txt",header=T,as.is = T, comment.char = "#" )->dat_kor

#### Remove participant #21 Not a Native speaker of Korean
dat_kor %>% filter(participant!=21) ->dat_kor

###### Filter our main task in language specific models ###### 
dat_en %>% filter(phase == "practice" | phase == "main") %>% select(responses,phase,baseline,word,factor_a,factor_b,level_a,level_b,Sex,Age,English,Korean,BirthCountry,ResidentCountry,KoreanFamiliarity,KoreanGendering,participant) %>% mutate(factor_b = if_else(factor_b == "Initial", "Final", "Initial")) -> dat_en_main

dat_kor %>% filter(phase == "practice" | phase == "main") %>% select(responses,phase,baseline,word,factor_a,factor_b,level_a,level_b,Sex,Age,English,Korean,BirthCountry,ResidentCountry,participant) %>% mutate(factor_b=if_else(factor_b == "Initial", "Final", "Initial")) -> dat_kor_main

###### Create combined file with language for combined analysis ###### 
dat_all_main = NULL
dat_en_main %>% select(responses,phase,baseline,word,factor_a,factor_b,level_a,level_b,Sex,Age,English,Korean,BirthCountry,ResidentCountry,participant) -> dat_en_main_b
dat_en_main_b$language="English"
dat_kor_main$language="Korean"
dat_all_main = rbind(dat_en_main_b,dat_kor_main)

###### Set variables to the correct factor type ######
dat_en_main$responses = as.integer(as.character(dat_en_main$responses))
dat_en_main$baseline = as.factor(dat_en_main$baseline)
dat_en_main$level_a = as.factor(dat_en_main$level_a)
dat_en_main$participant = as.factor(as.character(dat_en_main$participant))
dat_en_main$Sex = as.factor(dat_en_main$Sex)

dat_kor_main$participant = as.factor(as.character(dat_kor_main$participant))
dat_kor_main$responses = as.integer(as.character(dat_kor_main$responses))
dat_kor_main$baseline = as.factor(dat_kor_main$baseline)
dat_kor_main$level_a = as.factor(dat_kor_main$level_a)
dat_kor_main$Sex = as.factor(dat_kor_main$Sex)

dat_all_main$responses = as.integer(as.character(dat_all_main$responses))
dat_all_main$baseline = as.factor(dat_all_main$baseline)
dat_all_main$level_a = as.factor(dat_all_main$level_a)
dat_all_main$Sex = as.factor(dat_all_main$Sex)
dat_all_main$participant = as.factor(as.character(dat_all_main$participant))
dat_all_main$language = as.factor(dat_all_main$language)

#############################################
######### FACTOR 1 - VOWEL ROUNDING #########
#############################################

dat_all_main %>% filter(phase == "main", factor_a=="Rounding")%>% group_by(level_a,language) %>% summarize(m=mean(responses), sd=sd(responses)) -> rnd_summary
rnd_summary %>%  ggplot(aes(language,m, fill=level_a)) + geom_col(position="dodge") + xlab("Language") + ylab("Mean Rating") + theme_bw() + guides(fill=guide_legend(title="Rounding")) + ggtitle("Vowel Rounding") + scale_fill_manual(values=c("#228833","#BBBBBB")) + theme(legend.position="bottom")+ylim(0,6)+ geom_errorbar(aes(ymin=m-sd, ymax=m+sd), width=.2,position=position_dodge(.9))
plot of chunk auto-report
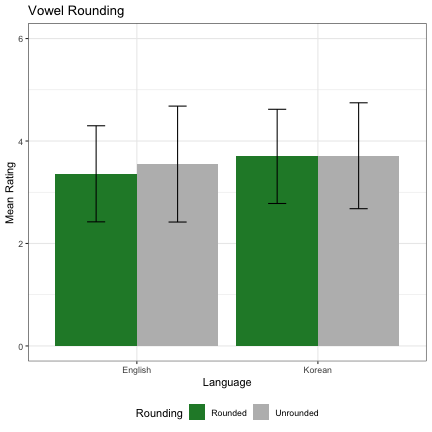
###### COMBINED ANALYSIS ###### 

### Filter for factor ###
dat_all_main %>% filter(factor_a=="Rounding") -> dat_all_main_rounding

## Create factor levels
dat_all_main_rounding$level_a = as.factor(as.character(dat_all_main_rounding$level_a))
dat_all_main_rounding$language = as.factor(as.character(dat_all_main_rounding$language))
contrasts(dat_all_main_rounding$level_a)=contrasts(dat_all_main_rounding$level_a)-1/2
contrasts(dat_all_main_rounding$Sex)=contrasts(dat_all_main_rounding$Sex)-1/2
contrasts(dat_all_main_rounding$language)=contrasts(dat_all_main_rounding$language)-1/2

## Regression Model
rounding_lm = lmer(responses~level_a*language+(1|baseline)+(1|Sex)+(1|participant), dat_all_main_rounding, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(rounding_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * language + (1 | baseline) + (1 | Sex) +  
##     (1 | participant)
##    Data: dat_all_main_rounding
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 923.7
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -3.06849 -0.68998  0.06437  0.57604  2.61143 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.037622 0.19397 
##  baseline    (Intercept) 0.029228 0.17096 
##  Sex         (Intercept) 0.003937 0.06275 
##  Residual                0.824248 0.90788 
## Number of obs: 340, groups:  participant, 34; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                  Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)                       3.61501    0.10738   2.26051  33.665 0.000422 ***
## level_aUnrounded                  0.06736    0.09864 300.00001   0.683 0.495217    
## languageKorean                    0.20770    0.11948  31.72624   1.738 0.091839 .  
## level_aUnrounded:languageKorean  -0.10972    0.19729 300.00001  -0.556 0.578522    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_Un lnggKr
## levl_Unrndd 0.000               
## languageKrn 0.043  0.000        
## lvl_Unrnd:K 0.000  0.059  0.000

###### ENGLISH PARTICIPANTS ###### 

### Filter for factor ###
dat_en_main %>% filter(factor_a=="Rounding") -> dat_en_main_rounding

## Create factor levels
dat_en_main_rounding$level_a = as.factor(as.character(dat_en_main_rounding$level_a))
contrasts(dat_en_main_rounding$level_a)=contrasts(dat_en_main_rounding$level_a)-1/2
contrasts(dat_en_main_rounding$Sex)=contrasts(dat_en_main_rounding$Sex)-1/2

## Regression Model
en_rounding_lm = lmer(responses~level_a+(1|baseline)+(1|participant), dat_en_main_rounding, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(en_rounding_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | participant)
##    Data: dat_en_main_rounding
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 477.3
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9806 -0.5614 -0.3025  0.5985  2.9118 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.044382 0.2107  
##  baseline    (Intercept) 0.007603 0.0872  
##  Residual                0.773496 0.8795  
## Number of obs: 180, groups:  participant, 18; baseline, 5
## 
## Fixed effects:
##                   Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)        3.50556    0.09101   6.08854  38.517 1.66e-08 ***
## level_aUnrounded   0.12222    0.13111 157.00000   0.932    0.353    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## levl_Unrndd 0.000

###### KOREAN PARTICIPANTS ###### 

### Filter for factor ###
dat_kor_main %>% filter(factor_a=="Rounding") -> dat_kor_main_rounding

## Create factor levels
dat_kor_main_rounding$level_a = as.factor(as.character(dat_kor_main_rounding$level_a))
contrasts(dat_kor_main_rounding$level_a)=contrasts(dat_kor_main_rounding$level_a)-1/2
contrasts(dat_kor_main_rounding$Sex)=contrasts(dat_kor_main_rounding$Sex)-1/2


## Regression model
kor_rounding_lm = lmer(responses~level_a+(1|baseline)+(1|participant), dat_kor_main_rounding, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(kor_rounding_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | participant)
##    Data: dat_kor_main_rounding
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 444.4
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.0755 -0.7274  0.1153  0.6417  2.1025 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.03564  0.1888  
##  baseline    (Intercept) 0.07390  0.2719  
##  Residual                0.86317  0.9291  
## Number of obs: 160, groups:  participant, 16; baseline, 5
## 
## Fixed effects:
##                  Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)        3.7062     0.1497   4.7418  24.762 3.37e-06 ***
## level_aUnrounded   0.0125     0.1469 139.0000   0.085    0.932    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## levl_Unrndd 0.000

#########################################
######### FACTOR 2 - VOWEL TYPE #########
#########################################

dat_all_main %>% filter(phase == "main", factor_a=="Vowel Type")%>% group_by(level_a,language) %>% summarize(m=mean(responses), sd=sd(responses)) -> vt_summary
vt_summary %>% mutate(uo = if_else(level_a=="Bright","o","u")) -> vt_summary_uo
vt_summary_uo %>%  ggplot(aes(language,m, fill=uo)) + geom_col(position="dodge") + xlab("Language") + ylab("Mean Rating") + theme_bw() + guides(fill=guide_legend(title="Vowel")) + ggtitle("Vowel Type") + scale_fill_manual(values=c("#4477AA","#EE6677")) + theme(legend.position="bottom")+ylim(0,6)+ geom_errorbar(aes(ymin=m-sd, ymax=m+sd), width=.2,position=position_dodge(.9))
plot of chunk auto-report
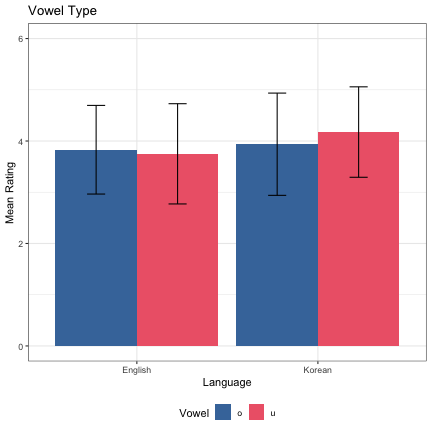
###### COMBINED ANALYSIS ###### 

### Filter for factor ###
dat_all_main %>% filter(factor_a=="Vowel Type") -> dat_all_main_vowel

## Create factor levels
dat_all_main_vowel$level_a = as.factor(as.character(dat_all_main_vowel$level_a))
dat_all_main_vowel$language = as.factor(as.character(dat_all_main_vowel$language))
contrasts(dat_all_main_vowel$level_a)=contrasts(dat_all_main_vowel$level_a)-1/2
contrasts(dat_all_main_vowel$language)=contrasts(dat_all_main_vowel$language)-1/2

## Regression Model
vowel_lm = lmer(responses~level_a*language+(1|Sex)+(1|participant), dat_all_main_vowel, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(vowel_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * language + (1 | Sex) + (1 | participant)
##    Data: dat_all_main_vowel
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 885.7
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.3416 -0.7607  0.1535  0.4911  2.8388 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.08725  0.2954  
##  Sex         (Intercept) 0.04875  0.2208  
##  Residual                0.71478  0.8454  
## Number of obs: 340, groups:  participant, 34; Sex, 2
## 
## Fixed effects:
##                             Estimate Std. Error        df t value Pr(>|t|)  
## (Intercept)                  3.97631    0.17217   0.97896  23.095   0.0293 *
## level_aDark                  0.06875    0.09186 304.00001   0.748   0.4548  
## languageKorean               0.30101    0.13814  31.23552   2.179   0.0370 *
## level_aDark:languageKorean   0.33750    0.18372 304.00001   1.837   0.0672 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_Dr lnggKr
## level_aDark 0.000               
## languageKrn 0.042  0.000        
## lvl_Drk:lnK 0.000  0.059  0.000

###### ENGLISH PARTICIPANTS ###### 

### Filter for factor ###
dat_en_main %>% filter(factor_a=="Vowel Type") -> dat_en_main_vowel

## Create factor levels
dat_en_main_vowel$level_a = as.factor(as.character(dat_en_main_vowel$level_a))
contrasts(dat_en_main_vowel$level_a)=contrasts(dat_en_main_vowel$level_a)-1/2
contrasts(dat_en_main_vowel$Sex)=contrasts(dat_en_main_vowel$Sex)-1/2


## Regression model
en_vowel_lm = lmer(responses~level_a+(1|baseline)+(1|Sex)+(1|participant), dat_en_main_vowel, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(en_vowel_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | Sex) + (1 | participant)
##    Data: dat_en_main_vowel
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 461.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.3355 -0.7881  0.2452  0.4385  1.5434 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.03970  0.1992  
##  baseline    (Intercept) 0.01355  0.1164  
##  Sex         (Intercept) 0.01665  0.1290  
##  Residual                0.70124  0.8374  
## Number of obs: 180, groups:  participant, 18; baseline, 5; Sex, 2
## 
## Fixed effects:
##             Estimate Std. Error       df t value Pr(>|t|)   
## (Intercept)   3.8097     0.1316   1.2896  28.951    0.009 **
## level_aDark  -0.1000     0.1248 157.0000  -0.801    0.424   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## level_aDark 0.000

###### KOREAN PARTICIPANTS ###### 

### Filter for factor ###
dat_kor_main %>% filter(factor_a=="Vowel Type") -> dat_kor_main_vowel

## Create factor levels
dat_kor_main_vowel$level_a = as.factor(as.character(dat_kor_main_vowel$level_a))
contrasts(dat_kor_main_vowel$level_a)=contrasts(dat_kor_main_vowel$level_a)-1/2
contrasts(dat_kor_main_vowel$Sex)=contrasts(dat_kor_main_vowel$Sex)-1/2

## Regression Model
kor_vowel_lm = lmer(responses~level_a+(1|baseline)+(1|Sex)+(1|participant), dat_kor_main_vowel, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(kor_vowel_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | Sex) + (1 | participant)
##    Data: dat_kor_main_vowel
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 408.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.6771 -0.6038 -0.0563  0.5363  2.6164 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.15652  0.3956  
##  baseline    (Intercept) 0.11179  0.3344  
##  Sex         (Intercept) 0.08451  0.2907  
##  Residual                0.61632  0.7851  
## Number of obs: 160, groups:  participant, 16; baseline, 5; Sex, 2
## 
## Fixed effects:
##             Estimate Std. Error       df t value Pr(>|t|)   
## (Intercept)   4.1422     0.2854   1.6610  14.516  0.00956 **
## level_aDark   0.2375     0.1241 139.0000   1.913  0.05776 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## level_aDark 0.000

#################################################
######### FACTOR 3 - SYLLABLE STRUCTURE #########
#################################################

dat_all_main %>% filter(phase == "main", factor_a=="Syllable Closure")%>% group_by(level_a,language) %>% summarize(m=mean(responses), sd=sd(responses)) -> sc_summary
sc_summary$level_a <- factor(sc_summary$level_a, levels = c("Both", "Initial", "Final","None"))
sc_summary %>%  ggplot(aes(language,m, fill=level_a)) + geom_col(position="dodge") + xlab("Language") + ylab("Mean Rating") + theme_bw() + guides(fill=guide_legend(title="Closed")) + ggtitle("Syllable Closure") + scale_fill_manual(values=c("#332288","#33BBEE", "#EE7733", "#EE3377")) + theme(legend.position="bottom")+ylim(0,6)+ geom_errorbar(aes(ymin=m-sd, ymax=m+sd), width=.2,position=position_dodge(.9))
plot of chunk auto-report
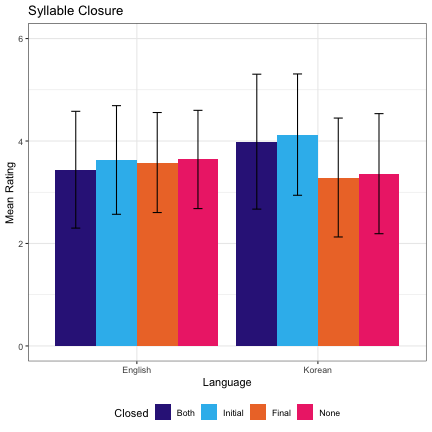
###### COMBINED ANALYSIS ###### 

### Filter for factor ###
dat_all_main %>% filter(factor_a=="Syllable Closure") -> dat_all_main_syllables

## Create factor levels
dat_all_main_syllables$level_a = as.factor(as.character(dat_all_main_syllables$level_a))
contrasts(dat_all_main_syllables$level_a)=cbind(none=c(-1/4,-1/4,-1/4, 3/4), two_one=c(2/3,-1/3,-1/3,0), initial_final=c(0,-1/2,1/2,0))
contrasts(dat_all_main_syllables$Sex)=contrasts(dat_all_main_syllables$Sex)-1/2

## Regression Model
syllable_lm = lmer(responses~level_a*language+(1|baseline)+(1|Sex)+(1|participant), dat_all_main_syllables, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(syllable_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * language + (1 | baseline) + (1 | Sex) +  
##     (1 | participant)
##    Data: dat_all_main_syllables
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 1991
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7520 -0.6442  0.0281  0.6467  3.4060 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.09571  0.3094  
##  baseline    (Intercept) 0.08311  0.2883  
##  Sex         (Intercept) 0.05578  0.2362  
##  Residual                1.00345  1.0017  
## Number of obs: 680, groups:  participant, 34; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                     Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)                           3.5981     0.2298   2.3908  15.654 0.001823 ** 
## level_anone                           0.1963     0.1219 636.0000   1.610 0.107902    
## level_atwo_one                       -0.2222     0.1293 636.0000  -1.718 0.086217 .  
## level_ainitial_final                  0.1111     0.1493 636.0000   0.744 0.457107    
## languageKorean                        0.1694     0.1325  31.1981   1.279 0.210293    
## level_anone:languageKorean           -0.6338     0.1777 636.0000  -3.566 0.000390 ***
## level_atwo_one:languageKorean         0.5035     0.1885 636.0000   2.671 0.007763 ** 
## level_ainitial_final:languageKorean   0.7264     0.2177 636.0000   3.337 0.000896 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_nn lvl_t_ lvl_n_ lnggKr lvl_:K lvl_t_:K
## level_anone  0.000                                            
## level_atw_n  0.000  0.000                                     
## lvl_ntl_fnl  0.000  0.000  0.000                              
## languageKrn -0.258  0.000  0.000  0.000                       
## lvl_nn:lngK  0.000 -0.686  0.000  0.000  0.000                
## lvl_tw_n:lK  0.000  0.000 -0.686  0.000  0.000  0.000         
## lvl_ntl_f:K  0.000  0.000  0.000 -0.686  0.000  0.000  0.000

###### ENGLISH PARTICIPANTS ###### 

### Filter for factor ###
dat_en_main %>% filter(factor_a=="Syllable Closure") -> dat_en_main_syllables

## Create factor levels
dat_en_main_syllables$level_a = as.factor(as.character(dat_en_main_syllables$level_a))
contrasts(dat_en_main_syllables$level_a)=cbind(none=c(-1/4,-1/4,-1/4, 3/4), two_one=c(2/3,-1/3,-1/3,0), initial_final=c(0,-1/2,1/2,0))
contrasts(dat_en_main_syllables$Sex)=contrasts(dat_en_main_syllables$Sex)-1/2

## Regression Model
en_syllable_lm = lmer(responses~level_a+(1|baseline)+(1|Sex)+(1|participant), dat_en_main_syllables, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(en_syllable_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | Sex) + (1 | participant)
##    Data: dat_en_main_syllables
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 970.1
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.79098 -0.64980  0.03679  0.67676  2.30062 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.07078  0.2660  
##  baseline    (Intercept) 0.08395  0.2897  
##  Sex         (Intercept) 0.03714  0.1927  
##  Residual                0.78600  0.8866  
## Number of obs: 360, groups:  participant, 18; baseline, 5; Sex, 2
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)   
## (Intercept)            3.5900     0.2042   2.4191  17.578   0.0013 **
## level_anone            0.1963     0.1079 335.0000   1.819   0.0698 . 
## level_atwo_one        -0.2222     0.1145 335.0000  -1.942   0.0530 . 
## level_ainitial_final   0.1111     0.1322 335.0000   0.841   0.4011   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_nn lvl_t_
## level_anone 0.000               
## level_atw_n 0.000  0.000        
## lvl_ntl_fnl 0.000  0.000  0.000

###### KOREAN PARTICIPANTS ###### 

### Filter for factor ###
dat_kor_main %>% filter(factor_a=="Syllable Closure") -> dat_kor_main_syllables

## Create factor levels
dat_kor_main_syllables$level_a = as.factor(as.character(dat_kor_main_syllables$level_a))
contrasts(dat_kor_main_syllables$level_a)=cbind(none=c(-1/4,-1/4,-1/4, 3/4), two_one=c(2/3,-1/3,-1/3,0), initial_final=c(0,-1/2,1/2,0))
contrasts(dat_kor_main_syllables$Sex)=contrasts(dat_kor_main_syllables$Sex)-1/2

## Regression Model
kor_syllable_lm = lmer(responses~level_a+(1|baseline)+(1|Sex)+(1|participant), dat_kor_main_syllables, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(kor_syllable_lm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a + (1 | baseline) + (1 | Sex) + (1 | participant)
##    Data: dat_kor_main_syllables
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 981
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7490 -0.6341 -0.0271  0.7084  3.4056 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.13952  0.3735  
##  baseline    (Intercept) 0.23106  0.4807  
##  Sex         (Intercept) 0.05949  0.2439  
##  Residual                1.12173  1.0591  
## Number of obs: 320, groups:  participant, 16; baseline, 5; Sex, 2
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            3.7599     0.3014   2.8699  12.477  0.00137 ** 
## level_anone           -0.4375     0.1367 297.0000  -3.200  0.00152 ** 
## level_atwo_one         0.2812     0.1450 297.0000   1.939  0.05341 .  
## level_ainitial_final   0.8375     0.1675 297.0000   5.001 9.76e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_nn lvl_t_
## level_anone 0.000               
## level_atw_n 0.000  0.000        
## lvl_ntl_fnl 0.000  0.000  0.000

#########################################################################
######### FACTOR 4A - INITIAL OBSTRUENT TYPE - INITIAL SYLLABLE #########
#########################################################################

dat_all_main %>% filter(phase == "main", factor_a=="Stop Type")%>% group_by(level_a,level_b,factor_b,language) %>% summarize(m=mean(responses), sd=sd(responses)) -> st_summary
st_summary$level_a <- factor(st_summary$level_a, levels = c("Fortis", "Lenis", "Asp"))
st_summary$factor_b <- factor(st_summary$factor_b, levels = c("Initial", "Final"))
st_summary %>% rename(vot = level_a, F0 = level_b, syllable = factor_b) -> st_summary
st_summary %>%  filter(syllable == "Initial") %>% ggplot(aes(language,m, fill=vot)) + geom_col(position="dodge") + xlab("Language") + ylab("Mean Rating") + theme_bw() + guides(fill=guide_legend(title="Obstruent")) + ggtitle("Obstruent Type - Initial Syllable") + theme(legend.position="bottom")+ylim(0,6)+ geom_errorbar(aes(ymin=m-sd, ymax=m+sd), width=.2,position=position_dodge(.9)) + facet_grid(.~F0, labeller = label_both) + scale_fill_manual(values=c("#DDCC77","#AA4499", "#44AA99"))
plot of chunk auto-report
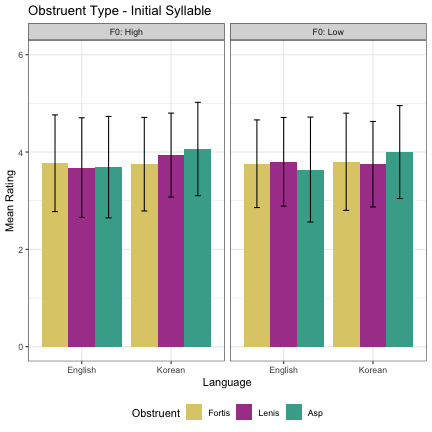
###### COMBINED ANALYSIS ###### 

### Filter for factor ###
dat_all_main %>% filter(factor_a=="Stop Type") -> dat_all_main_stops

## Create factor levels
dat_all_main_stops$level_a = as.factor(as.character(dat_all_main_stops$level_a))
dat_all_main_stops$level_b = as.factor(as.character(dat_all_main_stops$level_b))
dat_all_main_stops$factor_b = as.factor(as.character(dat_all_main_stops$factor_b))
dat_all_main_stops$language = as.factor(as.character(dat_all_main_stops$language))
contrasts(dat_all_main_stops$level_a)=cbind(asp=c(2/3,-1/3,-1/3), fortis_lenis=c(0,1/2,-1/2))
contrasts(dat_all_main_stops$level_b)=contrasts(dat_all_main_stops$level_b)-1/2
contrasts(dat_all_main_stops$factor_b)=contrasts(dat_all_main_stops$factor_b)-1/2
contrasts(dat_all_main_stops$Sex)=contrasts(dat_all_main_stops$Sex)-1/2
contrasts(dat_all_main_stops$language)=contrasts(dat_all_main_stops$language)-1/2

## Filter for initial syllable
dat_all_main_stops %>% filter(factor_b=="Initial") -> dat_all_main_stops_initial

## Regression Model
stops_lm_init = lmer(responses~level_a*level_b*language+(1|baseline)+(1|Sex)+(1|participant), dat_all_main_stops_initial, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(stops_lm_init)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b * language + (1 | baseline) + (1 |  
##     Sex) + (1 | participant)
##    Data: dat_all_main_stops_initial
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 2679.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.1289 -0.5740 -0.0273  0.6619  3.1815 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.060892 0.24676 
##  baseline    (Intercept) 0.114699 0.33867 
##  Sex         (Intercept) 0.009914 0.09957 
##  Residual                0.750977 0.86659 
## Number of obs: 1020, groups:  participant, 34; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                                Estimate Std. Error        df t value
## (Intercept)                                     3.81457    0.17514   4.59014  21.780
## level_aasp                                      0.07760    0.05766 971.99999   1.346
## level_afortis_lenis                            -0.02882    0.06658 971.99999  -0.433
## level_bLow                                     -0.01296    0.05436 971.99999  -0.238
## languageKorean                                  0.19326    0.10142  31.45105   1.906
## level_aasp:level_bLow                          -0.03576    0.11532 971.99999  -0.310
## level_afortis_lenis:level_bLow                  0.09653    0.13316 971.99999   0.725
## level_aasp:languageKorean                       0.28854    0.11532 971.99999   2.502
## level_afortis_lenis:languageKorean             -0.07986    0.13316 971.99999  -0.600
## level_bLow:languageKorean                      -0.10741    0.10872 971.99999  -0.988
## level_aasp:level_bLow:languageKorean            0.08403    0.23064 971.99999   0.364
## level_afortis_lenis:level_bLow:languageKorean   0.28194    0.26632 971.99999   1.059
##                                               Pr(>|t|)    
## (Intercept)                                   8.25e-06 ***
## level_aasp                                      0.1786    
## level_afortis_lenis                             0.6652    
## level_bLow                                      0.8116    
## languageKorean                                  0.0659 .  
## level_aasp:level_bLow                           0.7565    
## level_afortis_lenis:level_bLow                  0.4687    
## level_aasp:languageKorean                       0.0125 *  
## level_afortis_lenis:languageKorean              0.5488    
## level_bLow:languageKorean                       0.3235    
## level_aasp:level_bLow:languageKorean            0.7157    
## level_afortis_lenis:level_bLow:languageKorean   0.2900    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lnggKr lv_:_L lv__:_L lvl_:K lv__:K lv_L:K l_:_L:
## level_aasp  0.000                                                                        
## lvl_frts_ln 0.000  0.000                                                                 
## level_bLow  0.000  0.000  0.000                                                          
## languageKrn 0.027  0.000  0.000  0.000                                                   
## lvl_sp:lv_L 0.000  0.000  0.000  0.000  0.000                                            
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000  0.000                                     
## lvl_sp:lngK 0.000  0.059  0.000  0.000  0.000  0.000  0.000                              
## lvl_frts_:K 0.000  0.000  0.059  0.000  0.000  0.000  0.000   0.000                      
## lvl_bLw:lnK 0.000  0.000  0.000  0.059  0.000  0.000  0.000   0.000  0.000               
## lvl_sp:_L:K 0.000  0.000  0.000  0.000  0.000  0.059  0.000   0.000  0.000  0.000        
## lvl_f_:_L:K 0.000  0.000  0.000  0.000  0.000  0.000  0.059   0.000  0.000  0.000  0.000

###### ENGLISH PARTICIPANTS ###### 

### Filter for factor ###
dat_en_main %>% filter(factor_a=="Stop Type") -> dat_en_main_stops

## Create factor levels
dat_en_main_stops$level_a = as.factor(as.character(dat_en_main_stops$level_a))
dat_en_main_stops$level_b = as.factor(as.character(dat_en_main_stops$level_b))
dat_en_main_stops$factor_b = as.factor(as.character(dat_en_main_stops$factor_b))
contrasts(dat_en_main_stops$level_a)=cbind(asp=c(2/3,-1/3,-1/3), fortis_lenis=c(0,1/2,-1/2))
contrasts(dat_en_main_stops$level_b)=contrasts(dat_en_main_stops$level_b)-1/2
contrasts(dat_en_main_stops$factor_b)=contrasts(dat_en_main_stops$factor_b)-1/2
contrasts(dat_en_main_stops$Sex)=contrasts(dat_en_main_stops$Sex)-1/2

## Filter for initial syllable
dat_en_main_stops %>% filter(factor_b=="Initial") -> dat_en_main_stops_initial

## Regression Model
en_stops_lm_init = lmer(responses~level_a*level_b+(1|baseline)+(1|participant), dat_en_main_stops_initial, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(en_stops_lm_init)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b + (1 | baseline) + (1 | participant)
##    Data: dat_en_main_stops_initial
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 1479.8
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.84563 -0.65630  0.08365  0.59606  2.92279 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.01466  0.1211  
##  baseline    (Intercept) 0.06666  0.2582  
##  Residual                0.86314  0.9291  
## Number of obs: 540, groups:  participant, 18; baseline, 5
## 
## Fixed effects:
##                                 Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)                      3.70556    0.12548   4.42076  29.532    3e-06 ***
## level_aasp                      -0.06667    0.08481 513.00000  -0.786    0.432    
## level_afortis_lenis              0.01111    0.09793 513.00000   0.113    0.910    
## level_bLow                       0.04074    0.07996 513.00000   0.510    0.611    
## level_aasp:level_bLow           -0.07778    0.16962 513.00000  -0.459    0.647    
## level_afortis_lenis:level_bLow  -0.04444    0.19586 513.00000  -0.227    0.821    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lv_:_L
## level_aasp  0.000                             
## lvl_frts_ln 0.000  0.000                      
## level_bLow  0.000  0.000  0.000               
## lvl_sp:lv_L 0.000  0.000  0.000  0.000        
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000

###### KOREAN PARTICIPANTS ###### 

### Filter for factor ###
dat_kor_main %>% filter(factor_a=="Stop Type") -> dat_kor_main_stops

## Create factor levels
dat_kor_main_stops$level_a = as.factor(as.character(dat_kor_main_stops$level_a))
dat_kor_main_stops$level_b = as.factor(as.character(dat_kor_main_stops$level_b))
dat_kor_main_stops$factor_b = as.factor(as.character(dat_kor_main_stops$factor_b))
contrasts(dat_kor_main_stops$level_a)=cbind(asp=c(2/3,-1/3,-1/3), fortis_lenis=c(0,1/2,-1/2))
contrasts(dat_kor_main_stops$level_b)=contrasts(dat_kor_main_stops$level_b)-1/2
contrasts(dat_kor_main_stops$factor_b)=contrasts(dat_kor_main_stops$factor_b)-1/2
contrasts(dat_kor_main_stops$Sex)=contrasts(dat_kor_main_stops$Sex)-1/2

## Filter for Initial syllable
dat_kor_main_stops %>% filter(factor_b=="Initial") -> dat_kor_main_stops_initial

## Regression Model
kor_stops_lm_init = lmer(responses~level_a*level_b+(1|baseline)+(1|Sex)+(1|participant), dat_kor_main_stops_initial, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(kor_stops_lm_init)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b + (1 | baseline) + (1 | Sex) +  
##     (1 | participant)
##    Data: dat_kor_main_stops_initial
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 1146.3
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.2959 -0.6049 -0.0624  0.6118  2.9854 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.122329 0.34976 
##  baseline    (Intercept) 0.239958 0.48986 
##  Sex         (Intercept) 0.006349 0.07968 
##  Residual                0.565064 0.75171 
## Number of obs: 480, groups:  participant, 16; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                 Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)                      3.89632    0.24620   4.06585  15.826 8.34e-05 ***
## level_aasp                       0.22187    0.07278 455.00000   3.048  0.00243 ** 
## level_afortis_lenis             -0.06875    0.08404 455.00000  -0.818  0.41377    
## level_bLow                      -0.06667    0.06862 455.00000  -0.972  0.33181    
## level_aasp:level_bLow            0.00625    0.14557 455.00000   0.043  0.96577    
## level_afortis_lenis:level_bLow   0.23750    0.16809 455.00000   1.413  0.15835    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lv_:_L
## level_aasp  0.000                             
## lvl_frts_ln 0.000  0.000                      
## level_bLow  0.000  0.000  0.000               
## lvl_sp:lv_L 0.000  0.000  0.000  0.000        
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000

#######################################################################
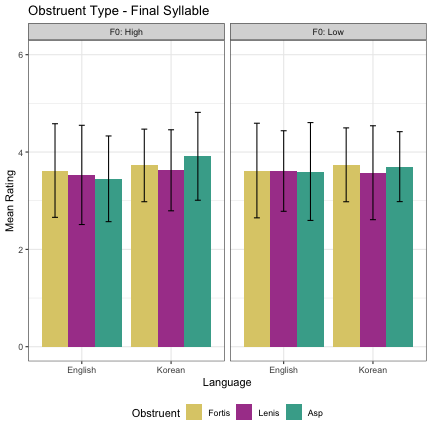
######### FACTOR 4B - INITIAL OBSTRUENT TYPE - FINAL SYLLABLE #########
#######################################################################

st_summary %>%  filter(syllable == "Final") %>%  ggplot(aes(language,m, fill=vot)) + geom_col(position="dodge") + xlab("Language") + ylab("Mean Rating") + theme_bw() + guides(fill=guide_legend(title="Obstruent")) + ggtitle("Obstruent Type - Final Syllable") + theme(legend.position="bottom")+ylim(0,6)+ geom_errorbar(aes(ymin=m-sd, ymax=m+sd), width=.2,position=position_dodge(.9)) + facet_grid(.~F0, labeller = label_both) + scale_fill_manual(values=c("#DDCC77","#AA4499", "#44AA99"))
plot of chunk auto-report
###### COMBINED ANALYSIS ###### 

## Filter for final syllable
dat_all_main_stops %>% filter(factor_b=="Final") -> dat_all_main_stops_final

## Regression Model
stops_lm_fin = lmer(responses~level_a*level_b*language+(1|baseline)+(1|Sex)+(1|participant), dat_all_main_stops_final, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(stops_lm_fin)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b * language + (1 | baseline) + (1 |  
##     Sex) + (1 | participant)
##    Data: dat_all_main_stops_final
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 2365.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.4318 -0.6119  0.0836  0.6354  3.3104 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.1127   0.3357  
##  baseline    (Intercept) 0.1358   0.3685  
##  Sex         (Intercept) 0.0152   0.1233  
##  Residual                0.5359   0.7321  
## Number of obs: 1020, groups:  participant, 34; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                                Estimate Std. Error        df t value
## (Intercept)                                     3.68955    0.19742   4.43046  18.689
## level_aasp                                      0.04115    0.04871 972.00000   0.845
## level_afortis_lenis                             0.09062    0.05624 972.00000   1.611
## level_bLow                                      0.00463    0.04592 972.00000   0.101
## languageKorean                                  0.11504    0.12501  31.44879   0.920
## level_aasp:level_bLow                          -0.01632    0.09742 972.00000  -0.168
## level_afortis_lenis:level_bLow                 -0.01875    0.11249 972.00000  -0.167
## level_aasp:languageKorean                       0.19896    0.09742 972.00000   2.042
## level_afortis_lenis:languageKorean              0.08125    0.11249 972.00000   0.722
## level_bLow:languageKorean                      -0.17593    0.09185 972.00000  -1.915
## level_aasp:level_bLow:languageKorean           -0.35486    0.19484 972.00000  -1.821
## level_afortis_lenis:level_bLow:languageKorean   0.16250    0.22498 972.00000   0.722
##                                               Pr(>|t|)    
## (Intercept)                                    2.2e-05 ***
## level_aasp                                      0.3985    
## level_afortis_lenis                             0.1074    
## level_bLow                                      0.9197    
## languageKorean                                  0.3645    
## level_aasp:level_bLow                           0.8670    
## level_afortis_lenis:level_bLow                  0.8677    
## level_aasp:languageKorean                       0.0414 *  
## level_afortis_lenis:languageKorean              0.4703    
## level_bLow:languageKorean                       0.0557 .  
## level_aasp:level_bLow:languageKorean            0.0689 .  
## level_afortis_lenis:level_bLow:languageKorean   0.4703    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lnggKr lv_:_L lv__:_L lvl_:K lv__:K lv_L:K l_:_L:
## level_aasp  0.000                                                                        
## lvl_frts_ln 0.000  0.000                                                                 
## level_bLow  0.000  0.000  0.000                                                          
## languageKrn 0.030  0.000  0.000  0.000                                                   
## lvl_sp:lv_L 0.000  0.000  0.000  0.000  0.000                                            
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000  0.000                                     
## lvl_sp:lngK 0.000  0.059  0.000  0.000  0.000  0.000  0.000                              
## lvl_frts_:K 0.000  0.000  0.059  0.000  0.000  0.000  0.000   0.000                      
## lvl_bLw:lnK 0.000  0.000  0.000  0.059  0.000  0.000  0.000   0.000  0.000               
## lvl_sp:_L:K 0.000  0.000  0.000  0.000  0.000  0.059  0.000   0.000  0.000  0.000        
## lvl_f_:_L:K 0.000  0.000  0.000  0.000  0.000  0.000  0.059   0.000  0.000  0.000  0.000

###### ENGLISH PARTICIPANTS ###### 

## Filter for final syllable
dat_en_main_stops %>% filter(factor_b=="Final") -> dat_en_main_stops_final

## Regression Model
en_stops_lm_fin = lmer(responses~level_a*level_b+(1|baseline)+(1|participant), dat_en_main_stops_final, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(en_stops_lm_fin)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b + (1 | baseline) + (1 | participant)
##    Data: dat_en_main_stops_final
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 1349.4
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0414 -0.6591  0.1353  0.6783  3.1664 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.11350  0.3369  
##  baseline    (Intercept) 0.09609  0.3100  
##  Residual                0.64318  0.8020  
## Number of obs: 540, groups:  participant, 18; baseline, 5
## 
## Fixed effects:
##                                 Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)                      3.61667    0.16345   6.64222  22.127  1.8e-07 ***
## level_aasp                      -0.05833    0.07321 513.00000  -0.797    0.426    
## level_afortis_lenis              0.05000    0.08454 513.00000   0.591    0.554    
## level_bLow                       0.09259    0.06902 513.00000   1.341    0.180    
## level_aasp:level_bLow            0.16111    0.14642 513.00000   1.100    0.272    
## level_afortis_lenis:level_bLow  -0.10000    0.16907 513.00000  -0.591    0.554    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lv_:_L
## level_aasp  0.000                             
## lvl_frts_ln 0.000  0.000                      
## level_bLow  0.000  0.000  0.000               
## lvl_sp:lv_L 0.000  0.000  0.000  0.000        
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000

###### KOREAN PARTICIPANTS ###### 

## Filter for Final syllable
dat_kor_main_stops %>% filter(factor_b=="Final") -> dat_kor_main_stops_final

## Regression Model
kor_stops_lm_fin = lmer(responses~level_a*level_b+(1|baseline)+(1|Sex)+(1|participant), dat_kor_main_stops_final, control = lmerControl(optimizer = "bobyqa", optCtrl=list(maxfun=2e6)))
summary(kor_stops_lm_fin)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: responses ~ level_a * level_b + (1 | baseline) + (1 | Sex) +  
##     (1 | participant)
##    Data: dat_kor_main_stops_final
## Control: lmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 2e+06))
## 
## REML criterion at convergence: 991.2
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.3468 -0.5463  0.0030  0.5696  2.9180 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  participant (Intercept) 0.10715  0.3273  
##  baseline    (Intercept) 0.19385  0.4403  
##  Sex         (Intercept) 0.04917  0.2218  
##  Residual                0.40384  0.6355  
## Number of obs: 480, groups:  participant, 16; baseline, 5; Sex, 2
## 
## Fixed effects:
##                                 Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)                      3.77855    0.26959   3.21454  14.016 0.000543 ***
## level_aasp                       0.14062    0.06153 455.00000   2.285 0.022745 *  
## level_afortis_lenis              0.13125    0.07105 455.00000   1.847 0.065350 .  
## level_bLow                      -0.08333    0.05801 455.00000  -1.437 0.151547    
## level_aasp:level_bLow           -0.19375    0.12306 455.00000  -1.574 0.116083    
## level_afortis_lenis:level_bLow   0.06250    0.14210 455.00000   0.440 0.660264    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) lvl_sp lvl_f_ lvl_bL lv_:_L
## level_aasp  0.000                             
## lvl_frts_ln 0.000  0.000                      
## level_bLow  0.000  0.000  0.000               
## lvl_sp:lv_L 0.000  0.000  0.000  0.000        
## lvl_frt_:_L 0.000  0.000  0.000  0.000  0.000

The R session information (including the OS info, R version and all packages used):

    sessionInfo()

## R version 3.6.2 (2019-12-12)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS Catalina 10.15.5
## 
## Matrix products: default
## BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
## 
## Random number generation:
##  RNG:     Mersenne-Twister 
##  Normal:  Inversion 
##  Sample:  Rounding 
##  
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
##  [1] ggpubr_0.3.0                  rpart_4.1-15                 
##  [3] forcats_0.4.0                 stringr_1.4.0                
##  [5] dplyr_0.8.4                   purrr_0.3.3                  
##  [7] readr_1.3.1                   tidyr_1.0.2                  
##  [9] tibble_2.1.3                  ggplot2_3.2.1                
## [11] tidyverse_1.3.0               lmerTest_3.1-1               
## [13] lme4_1.1-21                   Matrix_1.2-18                
## [15] LMERConvenienceFunctions_2.10 knitr_1.28                   
## 
## loaded via a namespace (and not attached):
##  [1] nlme_3.1-142            fs_1.3.1                lubridate_1.7.4        
##  [4] webshot_0.5.2           httr_1.4.1              numDeriv_2016.8-1.1    
##  [7] tools_3.6.2             backports_1.1.5         utf8_1.1.4             
## [10] R6_2.4.1                DBI_1.1.0               lazyeval_0.2.2         
## [13] mgcv_1.8-31             colorspace_1.4-1        manipulateWidget_0.10.0
## [16] withr_2.1.2             tidyselect_1.0.0        curl_4.3               
## [19] compiler_3.6.2          cli_2.0.1               rvest_0.3.5            
## [22] xml2_1.2.2              labeling_0.3            scales_1.1.0           
## [25] digest_0.6.23           foreign_0.8-72          minqa_1.2.4            
## [28] rio_0.5.16              pkgconfig_2.0.3         htmltools_0.4.0        
## [31] dbplyr_1.4.2            fastmap_1.0.1           highr_0.8              
## [34] maps_3.3.0              htmlwidgets_1.5.1       rlang_0.4.4            
## [37] readxl_1.3.1            rstudioapi_0.10         shiny_1.4.0            
## [40] farver_2.0.3            generics_0.0.2          jsonlite_1.6.1         
## [43] crosstalk_1.0.0         zip_2.0.4               car_3.0-6              
## [46] magrittr_1.5            dotCall64_1.0-0         Rcpp_1.0.3             
## [49] munsell_0.5.0           fansi_0.4.1             abind_1.4-5            
## [52] lifecycle_0.1.0         stringi_1.4.5           carData_3.0-3          
## [55] MASS_7.3-51.4           plyr_1.8.5              grid_3.6.2             
## [58] parallel_3.6.2          promises_1.1.0          crayon_1.3.4           
## [61] miniUI_0.1.1.1          lattice_0.20-38         cowplot_1.0.0          
## [64] haven_2.2.0             splines_3.6.2           hms_0.5.3              
## [67] pillar_1.4.3            boot_1.3-23             ggsignif_0.6.0         
## [70] reshape2_1.4.3          reprex_0.3.0            glue_1.3.1             
## [73] evaluate_0.14           data.table_1.12.8       modelr_0.1.5           
## [76] vctrs_0.2.2             spam_2.5-1              nloptr_1.2.1           
## [79] httpuv_1.5.2            cellranger_1.1.0        gtable_0.3.0           
## [82] assertthat_0.2.1        openxlsx_4.1.4          xfun_0.12              
## [85] LCFdata_2.0             mime_0.9                xtable_1.8-4           
## [88] broom_0.5.4             rstatix_0.5.0           later_1.0.0            
## [91] fields_10.3             rgl_0.100.47

    Sys.time()

## [1] "2020-07-14 21:09:15 EDT"